Hypercontractivity in $1$-dimension was described in the previous post. Hypercontractivity can be extended to the $n$-dimensional, which process is called $\textit{tensorization}$. Defining $s_{p}(x,y) := \inf \{\frac{q}{p}: 1 \lt q \leq p\}$ with $(p,q)$-hypercontractivity $P_{xy}$, the tensorization says \[ s_{p}(x^{n},y^{n}) = \max_{1 \leq i \leq n} \{ s_{p}(x_{i},y_{i}) \} \] for $(x_{i},y_{i})_{i=1}^{n} \sim \text{iid} \ P_{xy}$. The strategy is to apply hypercontractivity to each dimension, or each coordinate.
2-Dimension
The proof suffices to show this for the case where $n=2$. So, letting $f: \mathcal{X} \times \mathcal{X} \mapsto \mathbb{R}$ and $W^{2} := W_{1} \otimes W_{2}$ , we consider \[ W^{2} f(\mathscr{y}) = W^{2} f(\mathscr{y}_{1}, \mathscr{y}_{2}) = \mathop{\mathbb{E}}_{p_{x_{1} x_{2}|y_{1} y_{2}}} \left \lbrack f(x_{1}, x_{2}) |y_{1}= \mathscr{y}_{1}, y_{2}= \mathscr{y}_{2} \right \rbrack. \] The following figure illustrates how $W^{2}$ works.
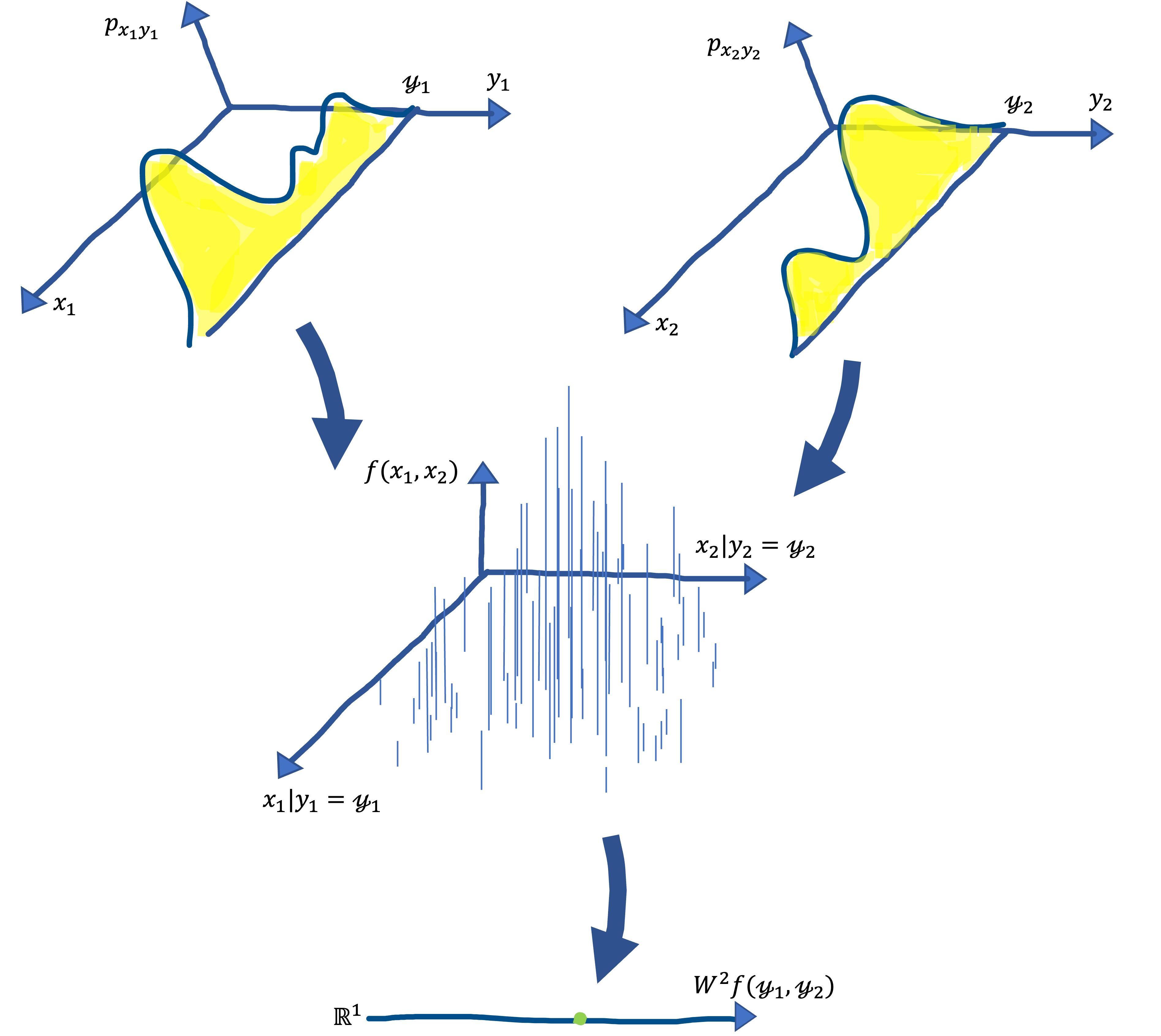
Note that $x_{1}$ depends only on $y_{1}$ and is independent of $y_{2}$ and $x_{2}$, and similarly, $x_{2}$ depends only on $y_{2}$ and is independent of $y_{1}$ and $x_{1}$
What we show is that $\forall f \in L_{p}(x_{1}, x_{2})$, \[ \color{green}{ \lVert W^{2} f \rVert_{p} } \leq \lVert f \rVert_{rp} \label{eq:1}\tag{1}, \] where $r$ is \[ r := s_{p}(x^{2},y^{2}) = \max \{ s_{p}(x_{1},y_{1}), s_{p}(x_{2},y_{2}) \}. \]
Fixing one coorinate
Let us see why Eq.$\,$($\ref{eq:1}$) is true. Using the definition of $W^{2} f$, we know that the LHS in Eq.$\,$($\ref{eq:1}$) is \[ \mathop{\mathbb{E}}_{p_{x_{1} x_{2} y_{1} y_{2}}} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{1} x_{2}|y_{1} y_{2}}} \left \lbrack f(x_{1}, x_{2}) | y_{1}, y_{2} \right \rbrack^{p} \right \rbrack = \color{green}{ \mathop{\mathbb{E}}_{p_{ y_{1} y_{2}}} \left \lbrack W^{2} f(y_{1}, y_{2})^{p} \right \rbrack } . \]
As mentioned at the beginnig, the strategy is to apply (1-dimension) hypercontractivity to each coordinate separately. So we first fix $y_{1}$ and take the expectation over $y_{2}$ only, followed by taking the expectation $y_{1}$. For convenience, for a function $g(z_{1}, z_{2})$, we denote it by $g_{z_{1}}( z_{2})$ while $z_{1}$ is being fixed. With this notation, we have \[ \color{green}{ \mathop{\mathbb{E}}_{p_{ y_{1} y_{2}}} \left \lbrack W^{2} f(y_{1}, y_{2})^{p} \right \rbrack } = \mathop{\mathbb{E}}_{p_{y_{1}}} \left \lbrack \mathop{\mathbb{E}}_{p_{y_{2}}} \left \lbrack W^{2} f_{y_{1}}( y_{2})^{p} \right \rbrack \right \rbrack = \mathop{\mathbb{E}}_{p_{y_{1}}} \left \lbrack \color{blue}{ \lVert W^{2}f_{y_{1}} \rVert_{p}^{\color{black}{p}} } \right \rbrack. \label{eq:2}\tag{2} \] The way we took in the proof of Hypercontractivity in the previous post was considering $\lVert Wf_{y} \rVert_{p}^{p}$ and applying Jensen’s inequality. Here we instead expand $\lVert Wf_{y} \rVert_{p}$ without the power of $p$, which can be written as \[ \color{blue}{ \lVert W^{2}f_{y_{1}} \rVert_{p} } = \mathop{\mathbb{E}}_{p_{y_{2}}} \left \lbrack W^{2} f_{y_{1}}( y_{2})^{p} \right \rbrack^\frac{1}{p} = \mathop{\mathbb{E}}_{p_{y_{2}}} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{1} x_{2}|y_{1} }} \left \lbrack f(x_{1}, x_{2})| y_{1}= \mathscr{y}_{1}, y_{2}) \right \rbrack^{p} \right \rbrack^\frac{1}{p}. \] As with $y_{1}, y_{2}$, we take a stepwise expectaion for $x_{1}, x_{2}$. Fixing $x_{1}$ and taking the expectaion over $x_{2}$, it can be written as \[ = \mathop{\mathbb{E}}_{p_{y_{2} }} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{1} | y_{1}= \mathscr{y}_{1} }} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{2} }} \left \lbrack f_{x_{1}}( x_{2})| y_{1}= \mathscr{y}_{1}, y_{2} \right \rbrack^{p} \right \rbrack \right \rbrack^\frac{1}{p}, \] and since $x_{2}$ is independent of $y_{1}$, it is \[ = \mathop{\mathbb{E}}_{p_{y_{2} }} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{1} | y_{1}= \mathscr{y}_{1} }} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{2} }} \left \lbrack f_{x_{1}}( x_{2})| y_{2} \right \rbrack^{p} \right \rbrack \right \rbrack^\frac{1}{p} = \mathop{\mathbb{E}}_{p_{y_{2} }} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{1} | y_{1}= \mathscr{y}_{1} }} \left \lbrack \left ( W_{2} f_{x_{1}}( y_{2}) \right )^{p} \right \rbrack \right \rbrack^\frac{1}{p} = \left \lVert \mathop{\mathbb{E}}_{p_{x_{1} | y_{1}= \mathscr{y}_{1} }} \left \lbrack W_{2} f_{x_{1}}( y_{2}) \right \rbrack \right \rVert_{p}. \] By applying Minkowski inequality, the RHS is bounded as \[ \leq \mathop{\mathbb{E}}_{p_{x_{1} | y_{1}= \mathscr{y}_{1} }} \left \lbrack \left \lVert W_{2} f_{x_{1}}( y_{2}) \right \rVert_{p} \right \rbrack. \] This is the function of $y_{2}$. Now we utilize hypercontractivity for the second cordinate, we can bound it as \[ \leq \color{red}{ \mathop{\mathbb{E}}_{p_{x_{1} | y_{1}= \mathscr{y}_{1} }} \left \lbrack \left \lVert f_{x_{1}}( x_{2}) \right \rVert_{rp} \right \rbrack }. \] Though we do not know whether the strength of hypercontractivity for the second cordinate is equal to $rp$ or smaller than $rp$, we use $rp$, the larger one.
Putting them togather
Pushing the obtained inequality back to Eq.$\,$($\ref{eq:2}$), we have \[ \color{green}{ \mathop{\mathbb{E}}_{p_{ y_{1} y_{2}}} \left \lbrack W^{2} f(y_{1}, y_{2})^{p} \right \rbrack } \left ( = \left \lVert W^{2}f \right \rVert_{p} \right ) \leq \mathop{\mathbb{E}}_{p_{ y_{1}}} \left \lbrack \color{red}{ \mathop{\mathbb{E}}_{p_{x_{1} | y_{1} }} \left \lbrack \left \lVert f_{x_{1}}( x_{2}) \right \rVert_{rp} \right \rbrack}^{p} \right \rbrack. \] Since we have already taken expectation over $y_{2}$ in the above, the expectation in the RHS is only over $y_{1}$, and thus we change the notation of $f_{x_{1}}( x_{2})$ to $g(x_{1})$. Now, using hypercontractivity for the first coordinate, we have \[ = \mathop{\mathbb{E}}_{p_{ y_{1}}} \left \lbrack \mathop{\mathbb{E}}_{p_{x_{1} | y_{1} }} \left \lbrack \left \lVert g({x_{1}}) \right \rVert_{rp} \right \rbrack^{p} \right \rbrack = \mathop{\mathbb{E}}_{p_{ y_{1}}} \left \lbrack W_{1} g({y_{1}})^{p} \right \rbrack \leq \left \lVert g({x_{1}}) \right \rVert_{rp}^{p}. \] Thus, \[ \left \lVert W^{2}f \right \rVert_{p} \leq \left \lVert g({x_{1}}) \right \rVert_{rp}^{p} = \mathop{\mathbb{E}}_{p_{ x_{1}}} \left \lbrack g({x_{1}})^{rp} \right \rbrack^{\frac{1}{rp}} = \mathop{\mathbb{E}}_{p_{ x_{1}}} \left \lbrack f_{x_{1}}(x_{2})^{rp} \right \rbrack^{\frac{1}{rp}} = \left \lVert f \right \rVert_{rp}, \] and therefore, $s_{p}(x^{2},y^{2}) \leq r$.