Hypercontractivity of Markov Kernel

Hypercontractivity is the notion that connects to Gaussian logarithmic Sobolev inequality and Data processing inequality. In this post we will see Hypercontractivity begining by describing contractivity as preparation. This post is based on the lecture by Himanshu Tyagi.

$L_p$ Norm

For $1\le p$ and any function $f:\mathcal{X}\mapsto \mathbb{R}$, the $L_p$ norm of $f$ is $$\Vert f{\Vert }_p={({\int }_{\mathcal{X}}|f(x){|}^{p}dx)}^{\frac{1}{p}}=\mathbb{E}{[f(x{)}^p]}^{\frac{1}{p}}.$$

Markov Kernel

Consider two random variable $x$ and $y$ with joint distribution $p_{xy}$. Letting $f:\mathcal{X}\mapsto \mathbb{R}$, we define $g:\mathcal{Y}\mapsto \mathbb{R}$ such that $$g(\mathcal{y}):=\mathbb{E}[f(x)|y=\mathcal{y}],$$ where $\mathcal{y}$ is the realization of $y$. The $\mathit{\text{channel}}$ is denoted by $W$. The $W$ is the operator that converts $f$ to $g$ as $g=Wf$, and it corresponds to Markov kernel. $W$ can be thought of as a transition matrix with an innumerable number of rows and columns. The following figure illustrates how $W$ works.

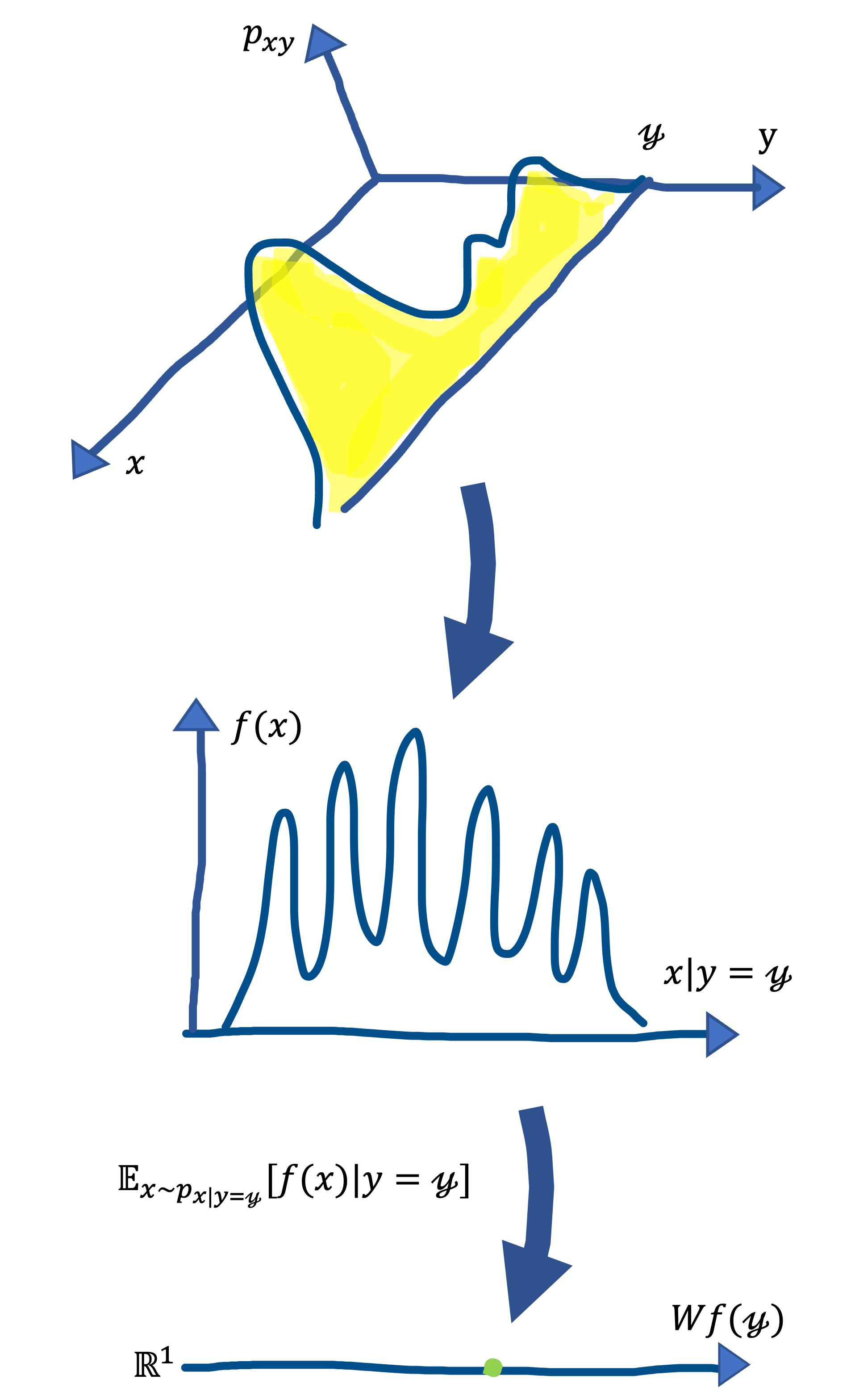
It would be ideal if we could get $f(y)$ directly, but what we can observe is a signal passsing through some noisy channel. The noise in the channel is decided by $P_{x|y}$ and depends on $y$. Thus, $$g(\mathcal{y})=Wf(\mathcal{y})=\underset{x\sim p_{x|y=\mathcal{y}}}{\mathbb{E}}[f(x)].$$

Contraction for $L_p$ Norm

In the above setting, $W$ is contraction for $L_p$ norm, that is, for $1\le p$, $$\begin{array}{}\text{(1)}& \Vert Wf{\Vert }_p\le \Vert f{\Vert }_p.\end{array}$$ The proof begins with $$\Vert Wf{\Vert }_p^p=\underset{x,y\sim p_{xy}}{\mathbb{E}}[\underset{x\sim p_{x|y=\mathcal{y}}}{\mathbb{E}}{[f(x)|y=\mathcal{y}]}^p].$$ By Jensen’s inequality, the RHS is bounded as $$\le \underset{x,y\sim p_{xy}}{\mathbb{E}}[\underset{x\sim p_{x|y=\mathcal{y}}}{\mathbb{E}}[f(x{)}^p|y=\mathcal{y}]].$$ Because the inner conditional expectation is canceled by the outer expectation, the above becomes $$=\underset{x,y\sim p_{xy}}{\mathbb{E}}[f(x{)}^p]]=\Vert f{\Vert }_p^p.$$

Hypercontractivity

While the contraction written as Eq.$$($\text{1}$) is the conversion between $p$-th norm and $p$-th norm, Hypercontractivity allows us to connect $p$-th norm to $q$-th norm where $q<p$. A joint distribution of $x$ and $y$, $P_{xy}$, is $(p,q)$-hypercontractivity for $1<q\le p<\mathrm{\infty }$, if $$\begin{array}{}\text{(2)}& \Vert Wf{\Vert }_p\le \Vert f{\Vert }_q\mathrm{\forall }f\in L_q(x).\end{array}$$ Since $L_p$ norm is non-decrease function of $p$, Eq.$$($\text{2}$) is stronger than Eq.$$($\text{1}$) when $q<p$.

Two-function hypercontractivity

Eq.$$($\text{2}$) holds if and only if $$\begin{array}{}\text{(3)}& \underset{x,y\sim p_{xy}}{\mathbb{E}}[f(x)g(y)]\le \Vert f{\Vert }_q\Vert g{\Vert }_{p^{\prime }}\mathrm{\forall }g\in L_p(y),\end{array}$$ where $p^{\prime }$ is Hölder conjugate of $p$, i.e., $p^{\prime }=\frac{p}{p-1}$.

From Eq.$$($\text{2}$) to Eq.$$($\text{3}$)

We first see the proof of the direction from Eq.$$($\text{2}$) to Eq.$$($\text{3}$). As $$\underset{x,y\sim p_{xy}}{\mathbb{E}}[f(x)g(y)]=\underset{x,y\sim p_{xy}}{\mathbb{E}}[Wf(y)g(y)],$$ by applying Hölder’s inequality, the RHS is bounded as $$\le \Vert f{\Vert }_p\Vert g{\Vert }_{p^{\prime }}.$$ Since we are assuming Eq.$$($\text{2}$), the above is bounded as $$\le \Vert f{\Vert }_q\Vert g{\Vert }_{p^{\prime }},$$ saying that Eq.$$($\text{3}$) is true.

From Eq.$$($\text{3}$) to Eq.$$($\text{2}$)

Suppose Eq.$$($\text{3}$) holds any $g$ and consider $f\in L_p(x)$. Then, $$\underset{x,y\sim p_{xy}}{\mathbb{E}}[Wf(y{)}^p]=\underset{x,y\sim p_{xy}}{\mathbb{E}}[Wf(y)Wf(y{)}^{p-1}]=\underset{x,y\sim p_{xy}}{\mathbb{E}}[\underset{x\sim p_{x|y=\mathcal{y}}}{\mathbb{E}}[f(x)]Wf(y{)}^{p-1}].$$ By cancellation by outer expectation over $p_{xy}$ similar to that seen above, the above becomes $$\begin{array}{}\text{(4)}& =\underset{x,y\sim p_{xy}}{\mathbb{E}}[f(x)Wf(y{)}^{p-1}].\end{array}$$ Defining $g(y):=Wf(y{)}^{p-1}$, we first derive $g\in L_{p^{\prime }}(y)$. Since $$\Vert g(y){\Vert }_{p^{\prime }}^{p^{\prime }}=\underset{x,y\sim p_{xy}}{\mathbb{E}}[(Wf(y{)}^{p-1}{)}^{p^{\prime }}]=\underset{x,y\sim p_{xy}}{\mathbb{E}}[Wf(y{)}^{p-1\frac{p}{p-1}}]=\underset{x,y\sim p_{xy}}{\mathbb{E}}[Wf(y{)}^p],$$ applying the contractivity, i.e., Eq.$$($\text{1}$), yields $$\underset{x,y\sim p_{xy}}{\mathbb{E}}[Wf(y{)}^p]\le \underset{x,y\sim p_{xy}}{\mathbb{E}}[f(x{)}^p]<\mathrm{\infty },$$ where the last inequality comes from the assumption of $f\in L_p(x)$, stating $g\in L_{p^{\prime }}(y)$.

Since $Wf(y{)}^{p-1}\in L_{p^{\prime }}(y)$, we can apply the assumption of Eq.$$($\text{3}$) to Eq.$$($\text{4}$), yielding $$\underset{x,y\sim p_{xy}}{\mathbb{E}}[f(x)Wf(y{)}^{p-1}]\le \Vert f{\Vert }_q\Vert W{f}^{p-1}{\Vert }_{p^{\prime }}.$$ The LHS is simply $$\underset{x,y\sim p_{xy}}{\mathbb{E}}[Wf(y{)}^p]=\Vert Wf{\Vert }_p^p.$$ Regarding the RHS, we know that $$\Vert W{f}^{p-1}{\Vert }_{p^{\prime }}={(\int |W{f}^{p-1}{|}^{p^{\prime }})}^{\frac{1}{p^{\prime }}}={(\int |Wf{|}^{(p-1)p^{\prime }})}^{\frac{1}{p^{\prime }}}={(\int |Wf{|}^p)}^{\frac{1}{p^{\prime }}}={(\int |Wf{|}^p)}^{\frac{1}{p}\frac{p}{p^{\prime }}}=\Vert Wf{\Vert }_p^{\frac{p}{p^{\prime }}}.$$ Putting them togather, we obtain $$\Vert Wf{\Vert }_p^p\le \Vert f{\Vert }_q\Vert Wf{\Vert }_p^{\frac{p}{p^{\prime }}}.$$ It is equal to $$\Vert Wf{\Vert }_p^{p-\frac{p}{p^{\prime }}}\le \Vert f{\Vert }_q,$$ and since $p-\frac{p}{p^{\prime }}=p-p\frac{p-1}{p}=1$, it becomes $$\Vert Wf{\Vert }_p\le \Vert f{\Vert }_q.$$ The proof of the direction from Eq.$$($\text{2}$) to Eq.$$($\text{3}$) is done.

In this post, we saw the $1$-dimensional case. We will see the extension to the $n$-dimensional case in the next post.