The Tukey median introduced in the previous post robustly estimates the true mean, i.e., the mean of the distribution before contaminated by outliers, or sample corruption. Specifically, letting $S \subset \mathbb{R}^{d}$ be an $\epsilon$-corrupted set of samples of size $n$ from $\mathcal{N}(\mu, \text{I}_{d})$, where $\epsilon \lt \frac{1}{6}$, there exists some universal constant $C \lt 0$ so that with probability $1 − \delta$, and we have that \[ \lVert \text{Tukey}(S) - \mu \rVert_{2} \leq \Phi^{-1} \left ( \frac{1}{2} + 3 \epsilon + C \sqrt{ \frac{d + \log 1/\delta}{n} } \right ). \label{eq:1}\tag{1} \] We saw that In particular, when $n$ is sufficiently large and $\epsilon$ is relatively small, the error in the mean estimation becomes \[ \lVert \text{Tukey}(S) - \mu \rVert_{2} \simeq \Phi^{-1} \left ( \frac{1}{2} + 3 \epsilon + \right ) = O(\epsilon). \label{eq:2}\tag{2} \] We will proof Eq.$\,$($\ref{eq:1}$).
$d$-dimension to 1-dimension with Gaussian CDF
Assuming $\forall \lVert v \rVert_{2} = 1$, we suppose \[ \frac{ |\{ x \in S_{g}: \langle x - \eta, v \rangle \geq 0\}|} {|S_{g}|} = \color{blue}{ \mathbb{P}_{x \sim \mathcal{N}(\mu, \text{I}_{d})} \left \lbrack \langle x - \eta, v \rangle \geq 0 \right \rbrack, } \label{eq:3}\tag{3} \] sayings that let’s ignore the concentraion of $\mathcal{N}(\mu, \text{I}_{d})$ for now. We first show that \[ \color{blue}{ \mathbb{P}_{x \sim \mathcal{N}(\mu, \text{I}_{d})} \left \lbrack \langle x - \eta, v \rangle \geq 0 \right \rbrack } = \color{green}{ \Phi(\langle \mu - \eta, v \rangle) }. \] As $\langle x - \eta, v \rangle \geq 0 $ can be written as \[ \langle x, v \rangle \geq \langle \eta, v \rangle \Leftrightarrow \langle x - \mu, v \rangle \geq \langle \eta - \mu, v \rangle, \] defining $z$ as $z := x - \mu$, we have $\langle z, v \rangle \geq \langle \eta - \mu, v \rangle$. Transformation from $x$ to $z$ is shown below:
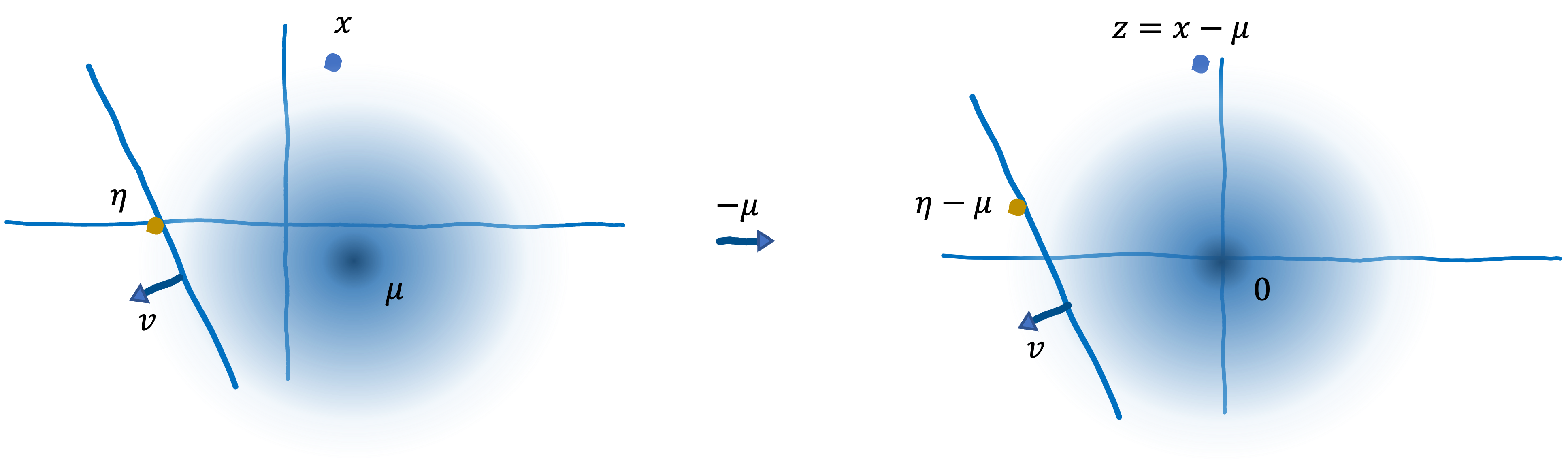
Thus, we have \[ \color{blue}{ \mathbb{P}_{x \sim \mathcal{N}(\mu, \text{I}_{d})} \left \lbrack \langle x - \eta, v \rangle \geq 0 \right \rbrack } = \mathbb{P}_{z \sim \mathcal{N}(0, \text{I}_{d})} \left \lbrack \langle z, v \rangle \geq \langle \mu - \eta, v \rangle \right \rbrack. \]
The $z$ satisfying $\langle z, v \rangle \geq \langle \eta - \mu, v \rangle$ corresponds to the points in the yellow region in the figure below.
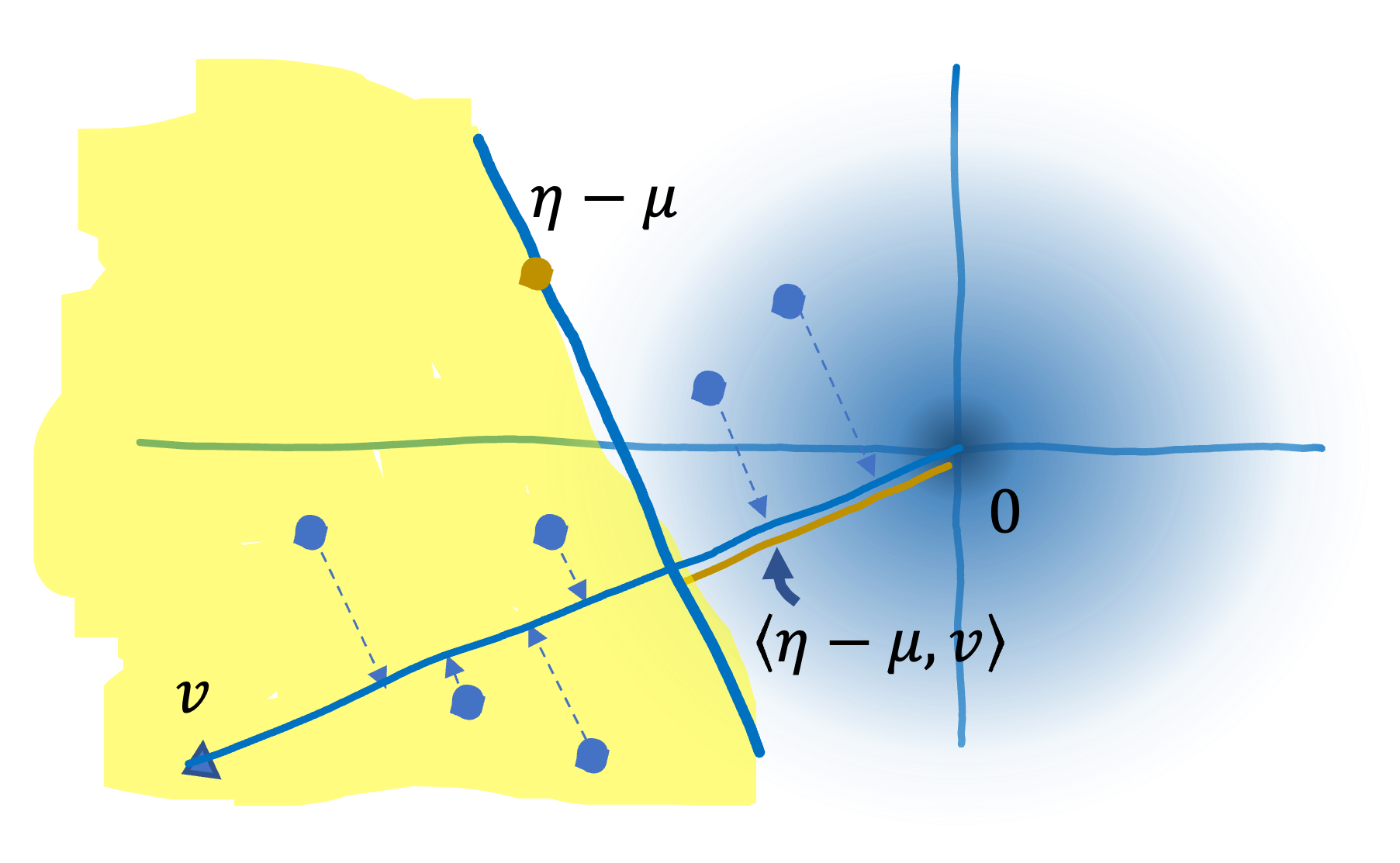
Then, as shown below,
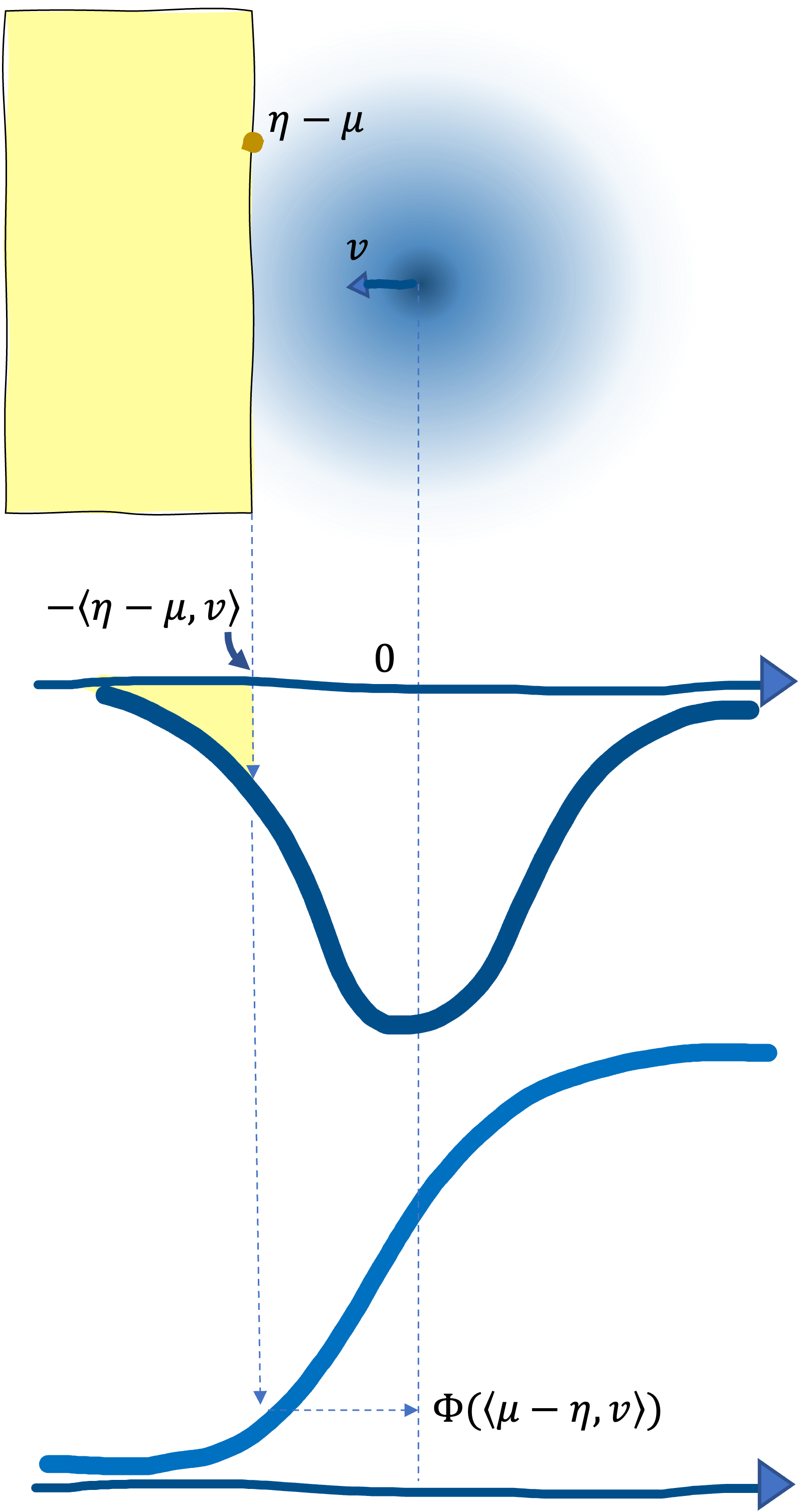
we know \[ \mathbb{P}_{z \sim \mathcal{N}(0, \text{I}_{d})} \left \lbrack \langle z, v \rangle \geq \langle \mu - \eta, v \rangle \right \rbrack = \color{green}{ \Phi(\langle \mu - \eta, v \rangle) }, \] and the proof of Eq.$\,$($\ref{eq:3}$) is done.
Rbustness of $\text{Tukey}(S)$
To derive Eqs.$\,$($\ref{eq:1}$) and $\,$($\ref{eq:2}$), we obtain two claims by using Eqs.$\,$($\ref{eq:3}$).
Claim 1
The first claim states that \[ \text{depth}(S, \mu) \geq \frac{1}{2} n - \epsilon n. \]
As $S = S_{g} \setminus S_{r} \cup S_{b}$, for all $\lVert v \rVert_{2} = 1$, we have \[ |\{ x \in S: \langle x - \mu, v \rangle \geq 0\}| = \color {red}{ |\{ x \in S_{g}: \langle x - \mu, v \rangle \geq 0\}| } + |\{ x \in S_{b}: \langle x - \mu, v \rangle \geq 0\}| - |\{ x \in S_{r}: \langle x - \mu, v \rangle \geq 0\}| . \] What we want now is the lower bound of the above, so we ignore the second term and take the maximamu of the third term utilizing the assumption of $ |\{ x \in S_{r}: \langle x - \mu, v \rangle \geq 0\}| \leq \epsilon n. $ Then, the above is bounded as \[ \geq \color {red}{ |\{ x \in S_{g}: \langle x - \mu, v \rangle \geq 0\}| } + 0 - \epsilon n. \]
From Eq.$\,$($\ref{eq:3}$), the first term can be written as \[ \color {red}{ |\{ x \in S_{g}: \langle x - \mu, v \rangle \geq 0\}| } = n \mathbb{P}_{x \sim \mathcal{N}(\mu, \text{I}_{d})} \left \lbrack \langle x - \mu, v \rangle \geq 0 \right \rbrack = n \Phi ( \langle \mu - \mu, v \rangle ) = n \Phi ( 0 ) = \frac{1}{2} n, \] and putting them together, we have \[ |\{ x \in S_{g}: \langle x - \mu, v \rangle \geq 0\}| \geq \frac{1}{2} n - \epsilon n. \] It is equivalent to the claim.
Claim 2
Suppose $\eta \in \mathbb{R}^{d}$ satisifies $\lVert \eta - \mu \rVert_{2} \leq \Phi^{-1}(\frac{1}{2} + 3 \epsilon) $. Then, $\text{depth}(S, \eta) \lt \frac{1}{2} - \epsilon$.
We will derive the upper bound and thus take inequality the other way around from Claim 1.
\[
|\{ x \in S: \langle \eta - \mu, v \rangle \geq 0\}|
=
\color {red}{
|\{ x \in S_{g}: \langle \eta - \mu, v \rangle \geq 0\}|
}
+
|\{ x \in S_{b}: \langle \eta - \mu, v \rangle \geq 0\}|
-
|\{ x \in S_{r}: \langle \eta - \mu, v \rangle \geq 0\}|
\]
can be bounded as
\[
\leq
\color {red}{
|\{ x \in S_{g}: \langle \eta - \mu, v \rangle \geq 0\}|
}
+ \epsilon n - 0
\leq
n \Phi ( \langle \eta - \mu, v \rangle ) + \epsilon n.
\]
Selecting $v$ as $v = \frac{\mu - \eta}{\lVert \mu - \eta \rVert_{2} }$, the above becomes
\[
= n \Phi ( - \lVert \mu - \eta \rVert_{2}) + \epsilon n.
\]
Applying the assumption $\lVert \eta - \mu \rVert_{2} \leq \Phi^{-1}(\frac{1}{2} + 3 \epsilon) $,
it is bounded as
\[
\leq n (\frac{1}{2} - 3 \epsilon) + \epsilon n = \frac{1}{2} n - 2\epsilon n
\leq \frac{1}{2} n - \epsilon n,
\]
and thus it says
\[
\text{depth}(S, \eta) \lt \frac{1}{2} - \epsilon .
\]
Derive Eq.$\,$($\ref{eq:2}$)
Recall $\text{Tukey}(S) = \underset{\eta}{\operatorname{argmax}} \text{depth}(S, \eta)$, it must be \[ \text{Tukey}(S) \geq \text{depth}(S, \mu) \geq \frac{1}{2} - \epsilon . \] On the other hand, Claim 2 says that if $\text{depth}(S, \eta) \geq \frac{1}{2} - \epsilon$, then $\lVert \eta - \mu \rVert_{2} \leq \Phi^{-1}(\frac{1}{2} + 3 \epsilon) $. Thus we obtain \[ \lVert \text{Tukey}(S) - \mu \rVert_{2} \leq \Phi^{-1} \left ( \frac{1}{2} + 3 \epsilon \right ) . \] We need to take a few step to achieve Eq.$\,$($\ref{eq:1}$), but we refer the reader to the course note of Jerry Li.