In 1-dimension, the median is more robust against the presence of outliers than the mean. A generalization of the 1-dimensional median to high dimensions is known as Tukey median; intuitively, it is a point that is a median in every projection. We will see the robustness of Tukey median in this post. This post is based on the course note by Jerry Li, and the italics in this post are quoted from the note.
$\epsilon$-corruption model
The problem we will tackle is called $\epsilon$-corruption model: Given samples from a distribution $D$, where an $\epsilon$-fraction have been corrupted, when can we recover statistics (e.g. mean, covariance) of $D$? Specifically, let $\epsilon \lt 1/2$ and $S = S_{g} \setminus S_{r} \cup S_{b}$ where $g$,$r$, and $b$ denote good, replaced, and bad, respectively.

Let $|S| = n$, $|S_{r}| = |S_{b}| = n \epsilon $, and $S_{g}$ is a set of i.i.d. samples from $\mathcal{N}(\mu, \text{I}_{d})$. What we can observe is $S$, and we assume that we know the value of $\epsilon$. We will estimate $\mu$ in this situation; in other words, we will output $\hat{\mu}$ that minimizes $\lVert \mu - \hat{ \mu} \rVert$.
Tukey depth
We first introduce Tukey depth. For any set of points $S \subset \mathbb{R}^{d}$ of size $n$, and any point $\eta \in \mathbb{R}^{d}$, Tukey depth is defined as \[ \text{depth}(S, \eta) = \inf_{\lVert v \rVert_{2} =1} \frac{1}{n} | \{ x \in S: \langle x - \eta, v \rangle \geq 0 \} |. \]
The following figure illustrates for $n=15$.
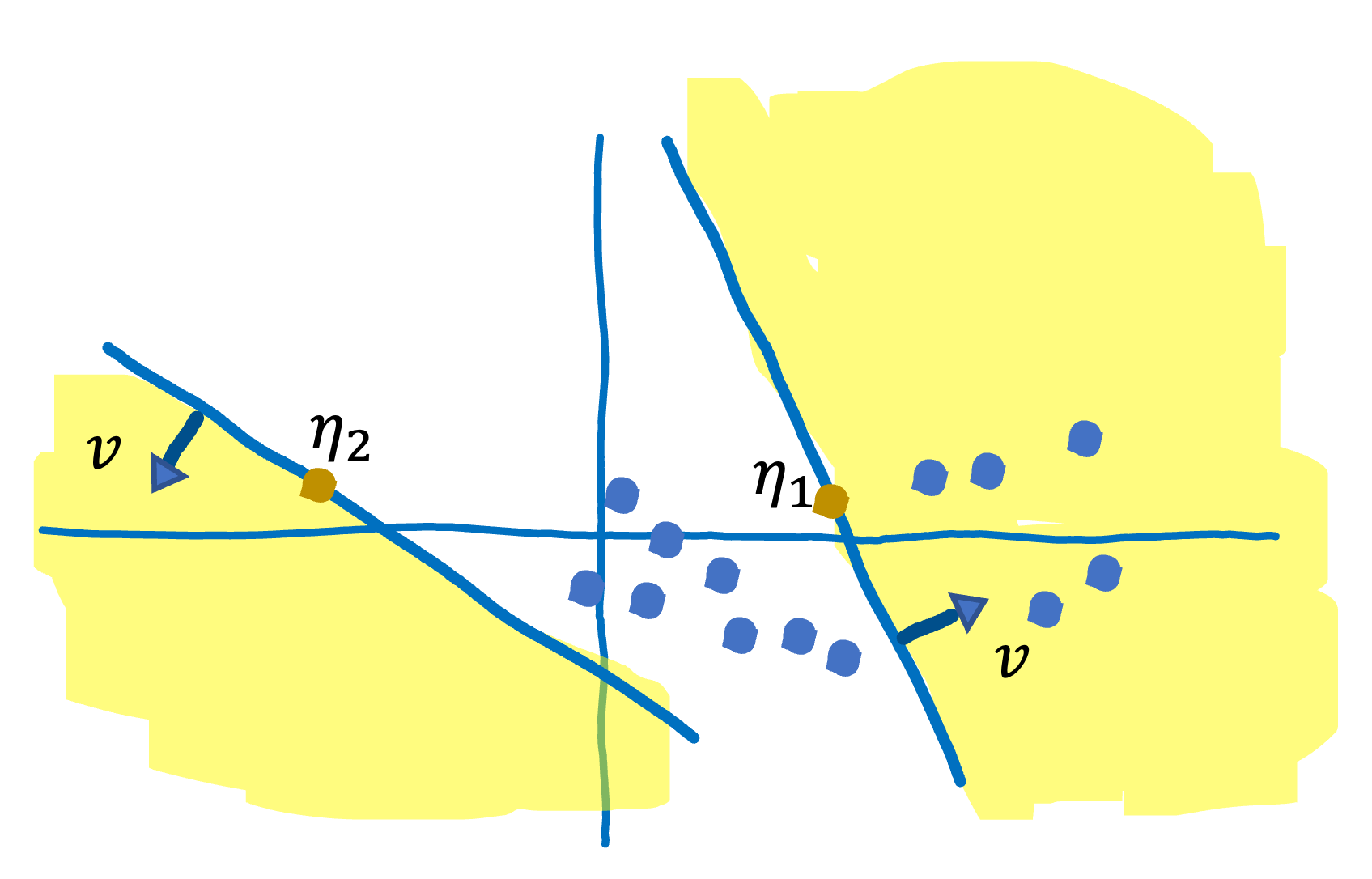
In this example, $\text{depth}(S, \eta_{1})=\frac{6}{15}$ and $\text{depth}(S, \eta_{2})=\frac{0}{15}$, and the half-spaces in yellow correspond to $x \in S$ for each. For a given point $\eta$, $\text{depth}(S, \eta)$ is the minimum number of points that lie in the yellow region while spinning the boundary line perpendicular to $v$ that passes through $\eta$. The larger the depth of $\eta$, the more central the point is with respect to the dataset $S$.
Tukey median
The Tukey median, which we will denote $\text{Tukey}(S)$, is simply defined as \[ \text{Tukey}(S) = \underset{\eta}{\operatorname{argmax}} \text{depth}(S, \eta). \] Observe that this is fundamentally a property of projections of the data. Thus this can hope to circumvent these dimensionality issues.
Robustness of Tukey median
We show that Tukey median can robustly estimate the true mean, i.e., the mean of the distribution before outliers, or corrupted samples, contaminated it. A situation where an $\epsilon$-fraction of samples from true distribution have been corrupted is called $\epsilon$-corruption. Let $S \subset \mathbb{R}^{d}$ be an $\epsilon$-corrupted set of samples of size $n$ from $\mathcal{N}(\mu, \text{I}_{d})$, where $\epsilon \lt \frac{1}{6}$. Then, there exists some universal constant $C \lt 0$ so that with probability $1 − \delta$, we have that \[ \lVert \text{Tukey}(S) - \mu \rVert_{2} \leq \Phi^{-1} \left ( \frac{1}{2} + 3 \epsilon + C \sqrt{ \frac{d + \log 1/\delta}{n} } \right ). \] The proof will follow in the next post, but before that, if this form is true, then we can say the following: if $n$ is sufficiently large and $\epsilon$ is relatively small, then the upper bound of the error between $\text{Tukey}(S)$ and $\mu$, i.e., the RHS, becomes $O(\epsilon)$. It is because under such a condition, the RHS $ \simeq \Phi^{-1} (\frac{1}{2} + 3 \epsilon)$, and $\Phi^{-1}(x)$ behaves almost linear around $x=\frac{1}{2}$, as
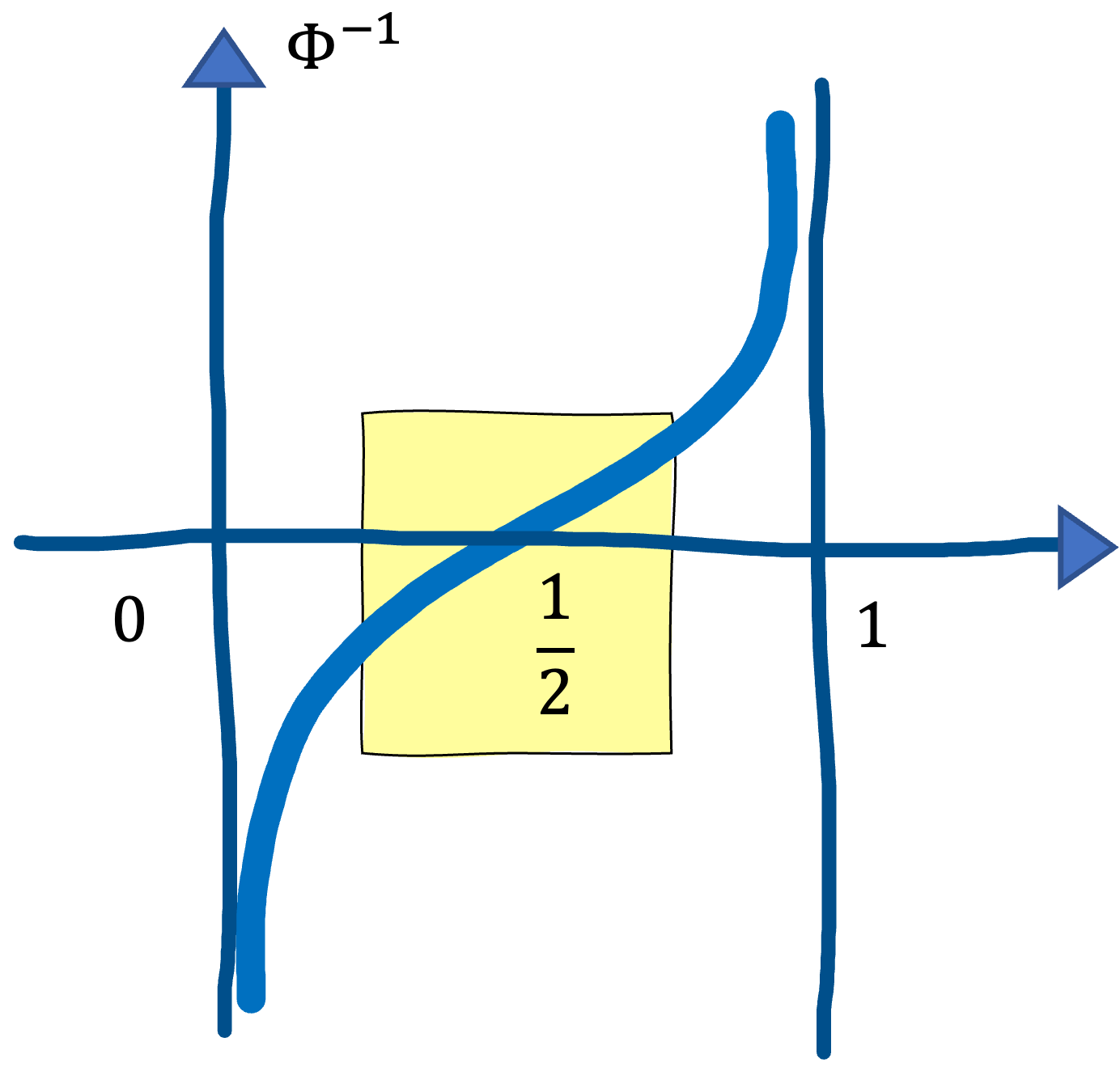
We derive the above in the next post. \[ \] \[ \] \[ \]