We show an application of Gaussian isoperimetric inequality to concentration inequalities of Lipschitz functions. Gaussian Isoperimetric Inequality and its derivation are described in this post. Suppose $ f: \mathcal{X} \mapsto \mathbb{R}$ is $L$-Lipschitz function where $\mathcal{X} \subset \mathbb{R}^n$, for all $x,y \in \mathcal{X}$, \[ | f(x) - f(y) | \leq L \lVert x - y \rVert_{2}. \] It is saying that to pull $f(x)$ and $f(y)$ apart $\epsilon$, $x$ and $y$ need to be pulled apart as much or more than $L \epsilon$.
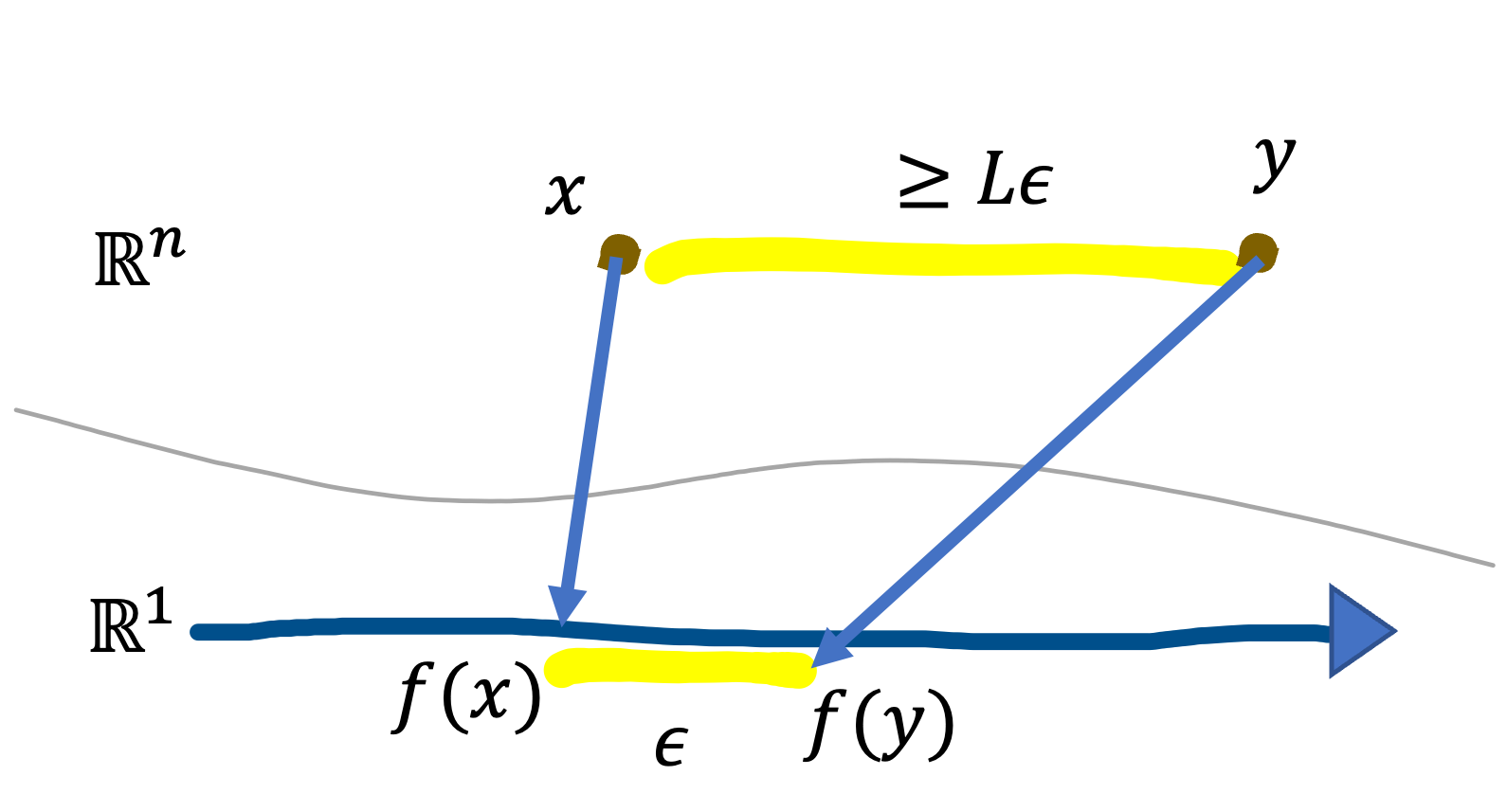
Connecting Lipschitz continuity to $\epsilon$-extension
For simplicity, let $L=1$ from here on. Letting $A \subset \mathcal{X}$ and $y \in A$, we consider $\epsilon$-extension of $A$, $A_{\epsilon}$. Then, we have \[ \{ x: f(x) -f(y) \geq \epsilon \} \subseteq \{ x: d(x, A) \geq \epsilon \} \label{eq:1}\tag{1}, \] where $d(x,A)$ denotes the distance from $x$ to the nearest point in $A$. This relationship can be easily understood by drawing a figure like the one below.
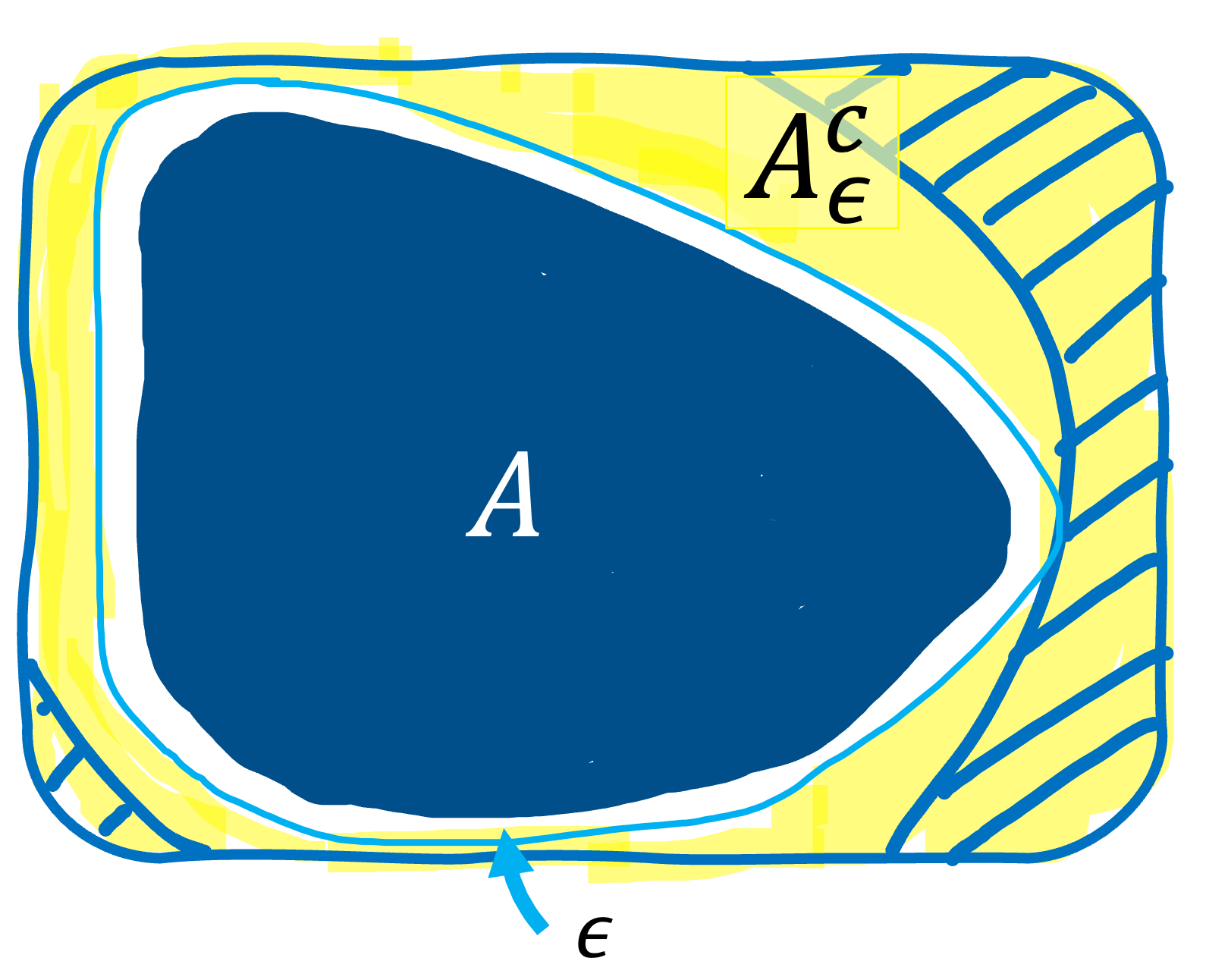
The figure depicts the entire $\mathcal{X}$. The area enclosed by the light blue line is $A_{\epsilon}$. The yellow area outside of $A_{\epsilon}$ is $A_{\epsilon}^{c}$, which corresponds to $\{ x: d(x, A) \geq \epsilon \}$ on the right-hand side in Eq.$\,$($\ref{eq:1}$); the shaded area in $A_{\epsilon}^{c}$ corresponds to $\{ x: f(x) -f(y) \geq \epsilon \}$ on the left-hand side in Eq.$\,$($\ref{eq:1}$).
Concentration of Lipschitz function on its median
Now, we impose one condition on $A$ as \[ A = \{ y: f(y) \leq M \} \] where $M$ denotes the median of $f(X)$ and $X$ is a random variable following the distribution $\mathbb{P}$ on $\mathcal{X}$.

The mountainous one on the bottom is a histogram of $f(X)$. Since $f(y) \leq M$, we can bound Eq.$\,$($\ref{eq:1}$) as \[ \{ x: f(x) - M \geq \epsilon \} \subseteq \{ x: f(x) -f(y) \geq \epsilon \} \subseteq \{ x: d(x, A) \geq \epsilon \}. \] Rewriting the above equation in probability measure, we obtain \[ \mathbb{P}(f(x) - M \geq \epsilon ) \leq \mathbb{P}( d(x, A) \geq \epsilon) = \mathbb{P}(A_{\epsilon}^{c}) \label{eq:2}\tag{2}. \] Defining $\alpha(\epsilon) := \sup_{A \subset \mathcal{X}, \mathbb{P}(A) \geq \frac{1}{2}} \mathbb{P}( d(x, A) \geq \epsilon)$, which is called the concentration function, we bound the left-hand side as \[ \mathbb{P}(f(x) - M \geq \epsilon ) \leq \alpha(\epsilon). \] It is saying that $\alpha(\epsilon)$ tells us that how fast $f$ concentrates on its median $M$.
Concentration on Gaussian measure
If we consider the situation where $\mathbb{P}$ is Gaussian measure $\gamma$, we can embody $\alpha(\epsilon)$. As the RHS of Eq.$\,$($\ref{eq:2}$) can be written as $\mathbb{P}(A_{\epsilon}^{c}) = 1 - \mathbb{P}(A_{\epsilon})$, we have \[ \mathbb{P}(f(x) - M \geq \epsilon ) \leq 1 - \gamma(A_{\epsilon}) = 1 - \gamma(A + \epsilon B). \] Applying the CDF of Gaussian $\Phi$ to both sides of Gaussian Isoperimetric Inequality as, \[ \Phi ( \Phi^{-1} ( \gamma(A + \epsilon B))) \geq \Phi ( \Phi^{-1} ( \gamma(A)) + \epsilon ), \]we obtain \[ \gamma(A + \epsilon B) \geq \gamma(A) + \Phi (\epsilon). \] Thus, \[ \mathbb{P}(f(x) - M \geq \epsilon ) \leq 1 - \gamma(A + \epsilon B) \leq 1- (\gamma(A) + \Phi (\epsilon)). \] Recall that $A = \{ y: f(y) \leq M \}$, and the shape of histogram I drew above is Gaussian (since we consider Gaussian measure), we have $\gamma(A) = \frac{1}{2}$. Therefore, \[ 1- (\gamma(A) + \Phi (\epsilon)) = \frac{1}{2} - \Phi (\epsilon) \leq 1 - \Phi (\epsilon) = \Phi (- \epsilon). \] As \[ \Phi (- \epsilon) = \frac{1}{\sqrt{2\pi}} \int_{\epsilon}^{\infty} \exp (-\frac{u^{2}}{2})du \leq \exp (-\frac{\epsilon^{2}}{2}), \] we finally obtain \[ \mathbb{P}(f(x) - M \geq L \epsilon ) \leq \Phi (- \frac{\epsilon}{L}) \leq \exp (-\frac{\epsilon^{2}}{2L^{2}}). \]