We saw in this post that if the logarithm of the moment generating function $ \psi_{Z - \mathop{\mathbb{E}}\left \lbrack Z \right \rbrack }(\lambda) = \log \mathop{\mathbb{E}} \exp \left (\lambda (Z - \mathop{\mathbb{E}} \left \lbrack Z \right \rbrack) \right ) $ for a random raviable $Z$ satisfies \[ \psi_{Z - \mathop{\mathbb{E}}\left \lbrack Z \right \rbrack }(\lambda) \leq \frac{ \lambda^{2}}{2} v \ \ \forall \lambda \gt 0, \label{eq:1}\tag{1} \] it equivalently indicates \[ \mathbb{P}\{ |Z - \mathop{\mathbb{E}} \left \lbrack Z \right \rbrack | \leq t\} \leq \exp( -\frac{t^{2}}{2 v}) \ \ \forall t \gt 0. \label{eq:2}\tag{2} \] Eq.$\,$($\ref{eq:2}$) says that such $Z$ behaves as the Gaussian random variable with variance $v$ and is heavily concentrated on its mean, $\mathop{\mathbb{E}} \left \lbrack Z \right \rbrack$, and thus the property, or behavior, of such $Z$ poses is called sub-Gaussianity. So, to say that $Z$ has the concentration property, we basically want to show Eq.$\,$($\ref{eq:1}$). Actually, Eq.$\,$($\ref{eq:1}$) can be shown indirectly in other ways, and one of them is the entropy method. In this post, as a preparation for the entropy method, we introduce two notions, the tilting measure and its relation to relative entropy.
Tilting measure
If $P$ is a probability measure on $\Omega$, and $Y: \Omega \rightarrow \mathbb{R}_{\geq 0}$ is any non-negative random variable such that $ \mathop{\mathbb{E}} \left \lbrack Y \right \rbrack = 1, $ define a new probability measure $Q = P_{Y}$ by tilting of the original measure $P$ with $Y$ as: \[ Q(A) = \mathop{\mathbb{E}} \left \lbrack Y 𝟙_{A}\right \rbrack, \ \ \mathop{\mathbb{E}_{Q}} \left \lbrack W \right \rbrack = \mathop{\mathbb{E}} \left \lbrack YW \right \rbrack \] where $\mathbb{E}$ denotes $\mathbb{E}_{P}$. We also write \[ \frac{dQ}{dP} = Y, \] which is called Radon-Nikodym derivative. Say Q is absolutely continuous with respect to $P$, which is denoted as $Q \lt \lt P $, if for any measurable $A$, $P(A) = 0 \Rightarrow Q(A) = 0$. In particular, Radon-Nikodym theorem states that if $Q \lt \lt P $, then there exists $Y$ such that $Q = P_{Y}$. The above is the copy from the lecture by Sudeep Kamath, but I share the intuition I got by the figure below.
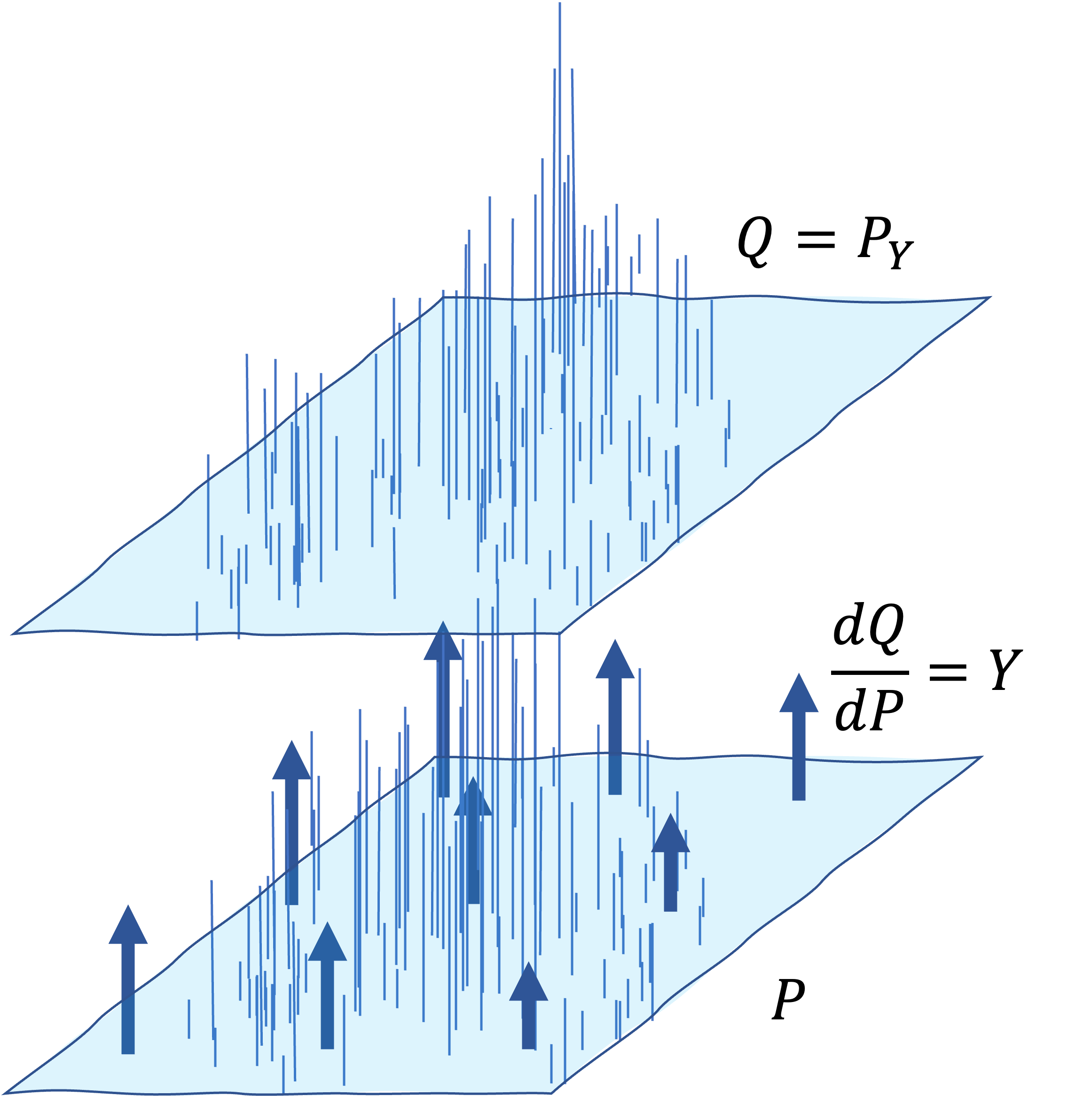
The original measure $P$ was tilted by arrows of different lengths in an upward direction, which correspond to $Y = \frac{dQ}{dP}$, resulting in smoothly tilted measure, $Q$.
Exponential tilting
Before we get to building a relationship with relative entropy, a little more preparation is in order. We consider tilting with \[ Y = \frac {e^{\lambda Z}} {\mathop{\mathbb{E}} \left \lbrack e^{\lambda Z} \right \rbrack }. \] The $Y$ is equal to the moment generating function of $Z$, and importantly, $\mathop{\mathbb{E}} \left \lbrack Y \right \rbrack = 1$. Then, the expectation of $Z$ over the measure $ Q = P_{ \frac {e^{\lambda Z}} {\mathop{\mathbb{E}} \left \lbrack e^{\lambda Z} \right \rbrack } } $ is \[ \mathop{\mathbb{E}_{Q}} \left \lbrack Z \right \rbrack = \int dQ \ Z = \int dP \frac {e^{\lambda Z}} {\mathop{\mathbb{E}} \left \lbrack e^{\lambda Z} \right \rbrack } Z = \frac{1} {\mathop{\mathbb{E}} \left \lbrack e^{\lambda Z} \right \rbrack } \int dP \ Z e^{\lambda Z} = \frac {\mathop{\mathbb{E}} \left \lbrack Z e^{\lambda Z} \right \rbrack } {\mathop{\mathbb{E}} \left \lbrack e^{\lambda Z} \right \rbrack } \]
Entropy
For convex function $\phi$, Jensen’s inequality says \[ \mathbb{E} \phi(X) - \phi(\mathbb{E} X) \geq 0. \] If $\phi = x^{2}$, we get $Var$. If $\phi = x \log x$, we get \[ \text{Ent}(X) := \mathbb{E} \left \lbrack X \log X \right \rbrack - \mathbb{E} \left \lbrack X \right \rbrack \log \mathbb{E} \left \lbrack X \right \rbrack \] Note that it is different from Shannon’s Entropy. Because of its convexity, \[ \text{Ent}(X) \geq 0, \] and another nice property is \[ \text{Ent}(aX) = a \text{Ent}(X), \label{eq:3}\tag{3} \] since $ \text{Ent}(aX) = \mathbb{E} \left \lbrack aX \log aX \right \rbrack - \mathbb{E} \left \lbrack aX \right \rbrack \log \mathbb{E} \left \lbrack aX \right \rbrack = a \mathbb{E} \left \lbrack X(\log a + \log X) \right \rbrack - a \mathbb{E} \left \lbrack X(\log a + \log \mathbb{E} \left \lbrack X \right \rbrack ) \right \rbrack . $
Connection to relative entropy
If $\mathbb{E} \left \lbrack Z \right \rbrack = 1$, \[ \text{Ent}(Z) = \mathbb{E} \left \lbrack Z \log Z\right \rbrack = D(P_{Z} \parallel P) \] where $D$ is relative entropy, or KL Divergence. Considering $Z = \frac{dQ}{dP}$ and the tilting with $Z$, the relative entropy between the original measure $P$ and $Q=P_{Z}$ is \[ D(Q \parallel P) = \int dQ \log \frac{dQ}{dP} = \int dP \frac{dQ}{dP} \log \frac{dQ}{dP} = \mathbb{E} \left \lbrack Z \log Z\right \rbrack. \] Therefore, by using the property of Eq.$\,$($\ref{eq:3}$), we obtain the following for the case where $\mathbb{E} \left \lbrack Z \right \rbrack \neq 1$: \[ \frac {\text{Ent}(Z) } { \mathbb{E} \left \lbrack Z \right \rbrack } = D(P_{\frac{Z}{\mathbb{E}Z}} \parallel P) \] The LHS tells us to what extent the measure $P$ is twisted. The entropy method is the method that examines the concentration using the above instead of directly handling the logarithm of the moment generating function.